서평) 수능까지 이어지는 초등 고학년 수학(기하1-1)

수능까지 이어지는 초등 고학년 수학

교과에서만 끝나지 않고 수능까지 바라보는 문제집. 수능적 사고를 하기엔 좀 이르지만 그래서 미리 이런 것들이 있다 익히고 가는 것도 괜찮을 듯 싶어 선택한 수능까지 이어지는 초등 고학년 수학 기하 파트 1-1

​

<도형의 기본은 점, 선, 면이다.>

초3때 직선과 반직선 그리고 선분에 대해서 자세히 배우기 시작한다. 솔직히 어릴적 직선과 선분의 차이를 배웠지 싶은데 기억이 안났다. 쭉 그어져 있는거 보면 무조건 직선이라고 말해서 구지 선분이라는 말을 많이 쓰지 않은거 같기도 하다.

​

​

<양 끝점의 개수로 선의 이름을 정한다.>

​

두 점 사이의 거리를 묻는 문제는 다양하게 나온다. 가장 짧은 길? 이란 말로 아이들을 헷갈리게 만들지만 개념을 정확하게 집고 넘어간다면 이런 문제도 끄떡 없지 싶다. 가장 짧은 길은 가장 빨리 가야 하고 가장 곧게 가야 빠른길이 될 수 있기 때문이다.

​

​

<거리의 비로 비례식을 만들 수 있다.>

​

비례식.. 왜 내항끼리의 곱고 외항끼리의 곱에 대해서는 자세히 나와 있지 않네... 그 개념이 먼저지 싶은데...

​

​

​

<두 반직선이 끝점에서 만나면 각을 이룬다.>

​

초등 3학년때 배운 각. 각을 표현 하는 방법과 읽는 방법 등이 나온다.

​

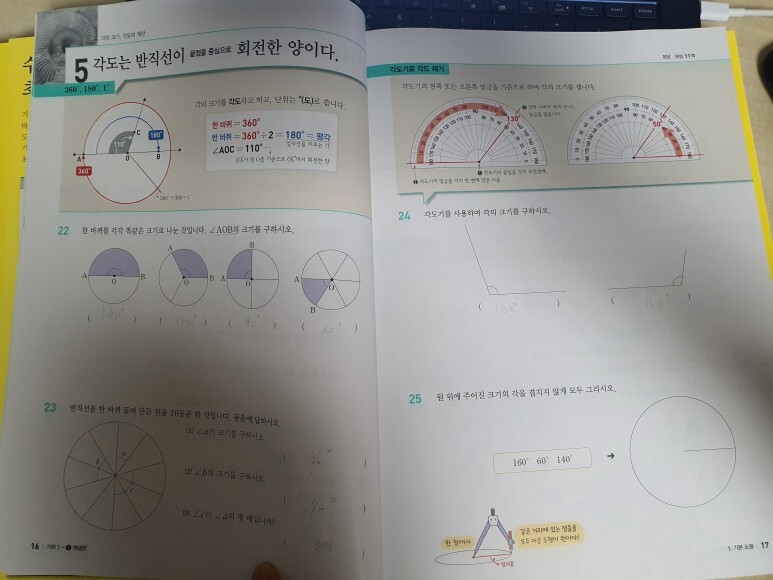
<각도는 반직선이 회전한 양이다.>

​

반직선이 한 바퀴를 돌면 360도가 되는 것만 알면 쉽게 문제를 풀 수있다. 거기에 더해서 평각과 예각 둔각도 확장해서 공부한는 것도 괜찮을 거 같다.

​

​

수능까지 이어지는 초등 고학년 수학시리즈 책은 총 6권으로 구성이 되어 있다.. 개념과 심화로 나뉘면서 총 12권이다. 내가 부족한 부분은 개념으로 다시 시작하고 기본 개념은 안다~ 하는 파트는 심화로 하면 되겠다.

하지만 개념을 다 안다고는 하지만 난 개념부터 쭉 풀면 좋겠다는 생각을 한다. 알기는 알지만 다시 한번 훑어 보면서 빠진 부분을 챙겨 보는 편을 더 좋아해서이다.

​

학기 중에는 기본 교과와 연산, 문장제, 사고력을 하고 방학때 쉬엄 쉬엄 선행과 함께 이 책을 하면 좋을거 같다는 생각이 들었다. 이제 초3이 된 학생들은 일단 교과에 충실하고 난 4학년 때 여름 방학 부터 개념으로 다지고 겨울 방학때는 심화를 하고.. 이런 식으로 하는 것도 괜찮을거 같다는 생각을 했다.

​

​

초등학생이 왜 수능을 미리 생각하고 문제집을 풀어야 하냐~ 라고 생각하시는 분도 계실텐데.. 난 수능시험 칠때 그 문제 유형이 갑자기 고등학교때 그렇게 문제집을 풀려고 하니 너무 힘이 들었다. 그래서 미리 이런 유형이 수능 문제다~ 라고 알려 주는 것도 좋겠다는 생각도 한다. 하지만 그게 초등학생인게 문제이긴 하지만... 너무 부담스럽게 하지 말고 개념을 정확히 짚고 넘어 간다는 생각으로 문제를 접해 주면 좋겠다.

#ne능률

#초등수학

#수학개념

#수능까지이어지는초등고학년수학

#책세상

#초등고학년

#수학기하

#기하개념편

​

ne능률 출판사로 부터 책을 무상으로 지원 받아 읽고 쓴 서평입니다.

​

​

태그#ne능률#초등수학#수학개념#수능까지이어지는초등고학년수학#책세상#초등고학년#수학기하#기하개념편 태그수정